在 B 站上偶然看到了这个系列 “从 0 开始的 C++ 算法课” ,感觉很适合入门,于是就跟着视频学习记录了一下。
有一对兔子,从出生后的第三个月起,每个月都生一对兔子,一对兔子成长到第三个月后每个月有生一对兔子,假如兔子都不死,问第 n 个月的兔子总数是多少对?

我们只关心每月的兔子对数,列出观察发现其实就是斐波那契数列

可以使用递归函数来解决,但需注意这个函数应该有两个起始项
int f(int n)
{
int res;
if (n == 1 || n == 2)
{
res = 1;
}
else
{
res = f(n - 1) + f(n - 2);
}
return res;
}
接下来我们用 for 循环打印前 6 个月的兔子对数
for (int i = 1; i <= 6; i++)
{
printf("month %d: %d\n", i, f(i));
}
但是这种算法有种缺陷,当月数变大时,程序计算结果的时间也就越长
我们以第 6 个月举例
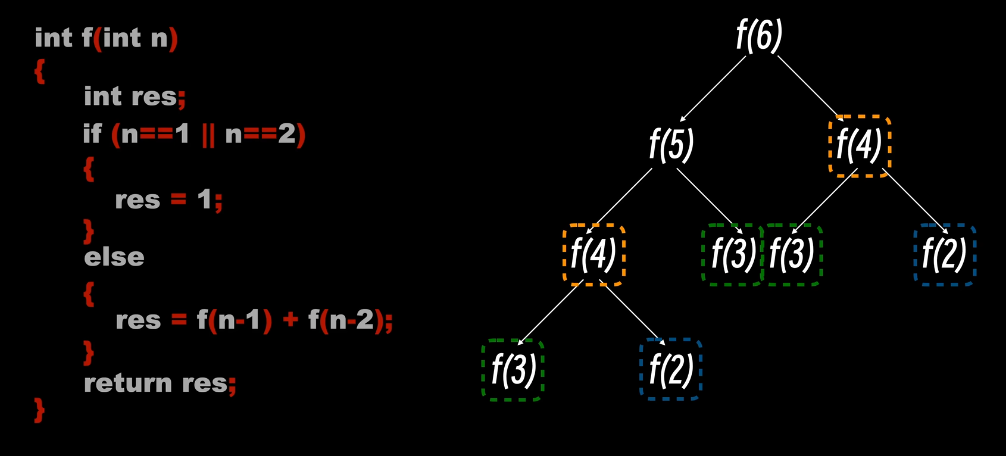
可以看到有很多项在被重复计算着,于是随着求解的项数越多,程序执行的效率也就越低,于是我们可以不使用递归,每一次只用计算一遍便可提升执行效率
定义一个整型数组 a 长度为 60 并初始化为 0,并将已经计算出结果月份存放在数组 a 中,可以使用 for 循环来完成数据的存放
long long a[60]={0};
a[1]=1;
a[2]=1;
for (int i = 3; i <= 50; i++)
{
a[i]=a[i-1]+a[i-2];
}
然后试着用 for 循环将前 50 月的结果全部输出
for (int i = 1; i <= 50; i++)
{
printf("month %d: %lld\n", i, a[i]);
}
可以明显地感受出差别,这种方式我们称之为递推,在数学中递推式同理
在墙角按照规律堆放着一些完全相同的正方体小块,只要知道层数就可以知道所有小块的数量
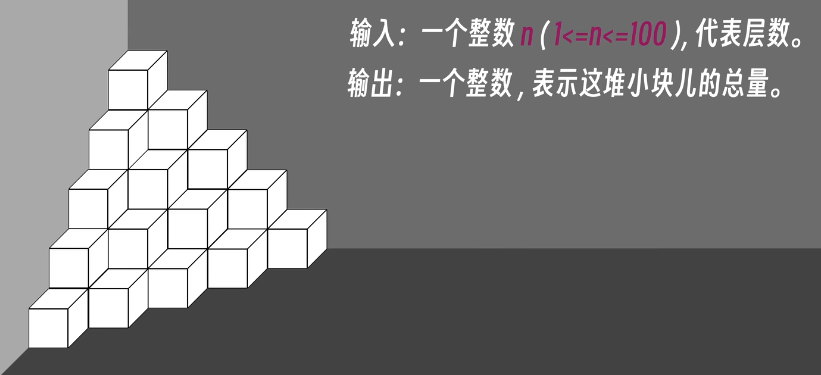
这里的规律就是除第一层,每一层都比上一层多了层数个的小块,可用 for 循环实现,记得初始化 level 和 sum 的值
for (int i = 2; i <= n; i++)
{
level = level + i;
sum = sum + level;
}
完整代码如下
#include <stdio.h>
int main()
{
int level = 1;
int sum = 1;
int n;
printf("Please enter a value for 'n': ");
scanf("%d", &n);
for (int i = 2; i <= n; i++)
{
level = level + i;
sum = sum + level;
}
printf("%d", sum);
return 0;
}
关于递推的两道习题

题 1
如果第十天有 1 个,那么第九天应该有 4 个,所以递推式如下
第 n 项 = (第 n+1 项 + 1) *2
全部代码如下
#include <stdio.h>
int main()
{
int a[15] = {0};
a[10] = 1;
for (int i = 9; i >= 1; i--)
{
a[i] = (a[i + 1] + 1) * 2;
}
printf("%d", a[1]);
return 0;
}
题 2
可以观察到分子分母都是斐波那契数列,于是我们可以用一个数组同时表示分子分母
全部代码如下
#include <stdio.h>
int main()
{
int a[35] = {0};
a[1] = 1;
a[2] = 1;
for (int i = 3; i <= 35; i++)
{
a[i] = a[i - 1] + a[i - 2];
}
int n;
printf("Please enter a value fot 'n'(1 <= n <= 30): ");
scanf("%d", &n);
double b[40] = {0};
double sum = 0;
for (int i = 1; i <= n; i++)
{
b[i] = (double)a[i] / a[i + 1];
sum = sum + b[i];
}
printf("%.3f", sum);
return 0;
}
