第02期 | 递推算法 | 经典题型解析 | 过河卒问题（递推算法求解）

算法·B站 - 这篇文章属于一个选集。

§ : 第00期 | 环境搭建 & 递归 (一) | 基本数列递归

§ : 第01期 | 递归(二) | 递归函数的缺陷 && 引出递推算法

§ : 本文

在 B 站上偶然看到了这个系列 “从 0 开始的 C++ 算法课” ，感觉很适合入门，于是就跟着视频学习记录了一下。

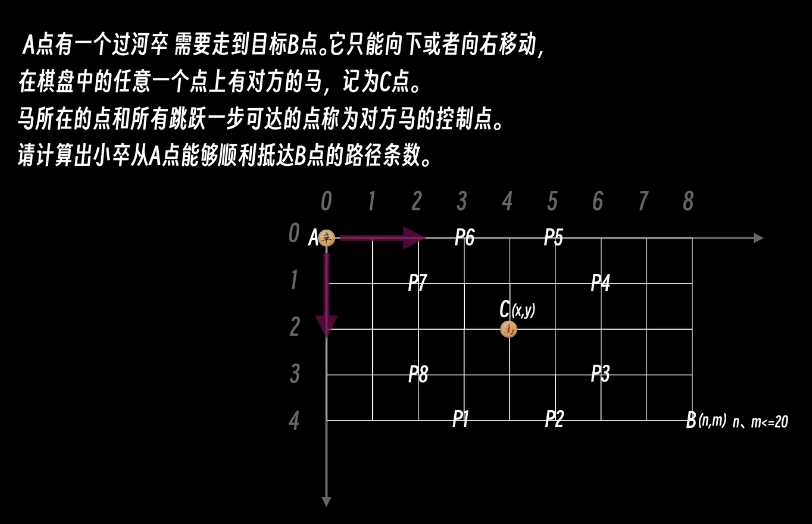
原系列视频作者链接【从0开始的C++算法课】第02期 | 递推算法 | 经典题型解析 | 过河卒问题（递推算法求解）

要求：

输入：B 点坐标 (n,m)一级对方马 C 的坐标 (x,y) （马的坐标一定在棋盘范围之内，但可以落在边界上）

输出：小卒从 A 点到 B 点的路径条数

输入样例：6 6 3 2

输出样例：17

卒的行走规则只有向右和向下，当不考虑马的情况简单分析如下

B 点和 A 点在同一行时路径只有 1 条
B 点和 A 点在同一列时路径只有 1 条
当 B 点在棋盘中间时，例如在 (1,1) 时，共有先向下再向右或者先向右再向下两条路径
当 B 点在 (1,2) 时，共有 3 条路径

分析可得，当 B 在中央时，路径条数总数是到达 B 所在位置上方和所在位置左方路径条数相加所得。想要知道到达上边或者左边的路径数就需要知道更上边或者更左边的路径数，可用递推表示。

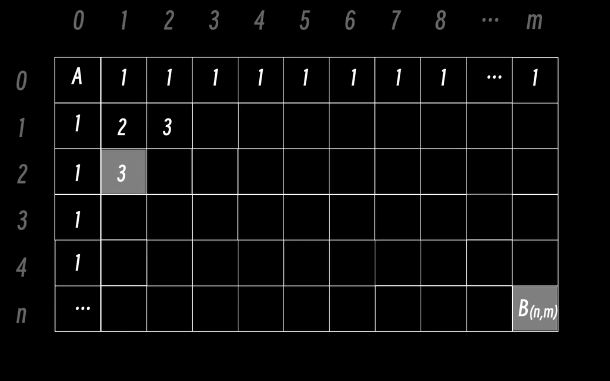
由于设计到坐标一般选择二维数组进行储值：数组名 [行数 n] [列数 m]

并且提前规定 n = 0 或 m = 0 时数组的值为 1，便可实现递推

int a[30][30] = {0};
int n, m;
printf("Please enter two value for 'n' and 'm': ");
scanf("%d %d", &n, &m);

for (int i = 0; i <= n; i++)
{
        for (int j = 0; j <= m; j++)
        {
                if (i == 0 && j == 0)
                {
                        continue;
                }
                if (i == 0 || j == 0)
                {
                        a[i][j] = 1;
                }
                else
                {
                        a[i][j] = a[i - 1][j] + a[i][j - 1];
                }
        }
}

以上只完成了没有马的情况下到达 B 点的路径条数，还需将马所在的 C 点及马的控制点 P 筛选出来

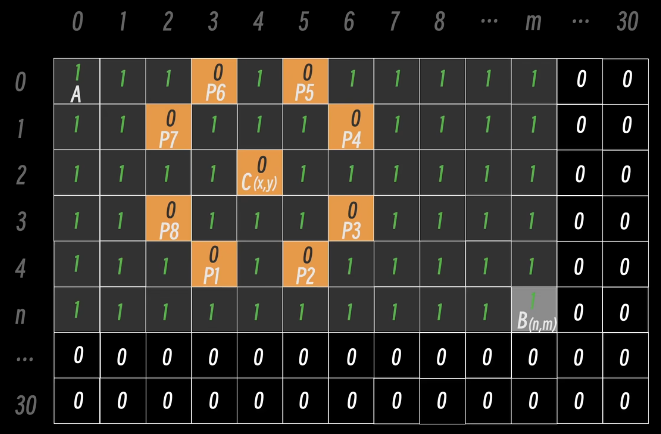
我们可提前将整个 B 点所在的表格中数组标记为 1 再将 C 点及 P 点数组的值标记为 0，需要注意

标记点是否存在于 B 点所在表格之内即阴影部分
标记点是否超出棋盘范围

可用简单的 if 语句判断

以及马的本身也为 0

但是如果当有任意一个马的控制点 P 占据了第 0 行和第 0 列的位置，就不能之间将第 0 行和第 0 列标记为 1 了，因为会被 P 点阻挡

分析表格后发现，第 0 行的每个位置的值都等于它左边的值，第 0 列的每个位置的值都等于它上方的值

完整修改代码如下：

#include <stdio.h>

int main()
{
    int a[30][30] = {0};
    int n, m, x, y;
    printf("Please enter two value for 'n' and 'm': ");
    scanf("%d %d", &n, &m);
    printf("Please enter two value for 'x' and 'y': ");
    scanf("%d %d", &x, &y);

    for (int i = 0; i <= n; i++)
    {
        for (int j = 0; j <= m; j++)
        {
            a[i][j] = 1;
        }
    }

    a[x][y] = 0;
    if (x + 2 <= n && y - 1 >= 0)
    {
        a[x + 2][y - 1] = 0;
    } // P1
    if (x + 2 <= n && y + 1 <= m)
    {
        a[x + 2][y + 1] = 0;
    } // P2
    if (x + 1 <= n && y + 2 <= m)
    {
        a[x + 1][y + 2] = 0;
    } // P3
    if (x - 1 >= 0 && y + 2 <= m)
    {
        a[x - 1][y + 2] = 0;
    } // P4
    if (x - 2 >= 0 && y + 1 >= 0)
    {
        a[x - 2][y + 1] = 0;
    } // P5
    if (x - 2 >= 0 && y - 1 >= 0)
    {
        a[x - 2][y - 1] = 0;
    } // P6
    if (x - 1 >= 0 && y - 2 >= 0)
    {
        a[x - 1][y - 2] = 0;
    } // P7
    if (x + 1 <= n && y - 2 >= 0)
    {
        a[x + 1][y - 2] = 0;
    } // P8

    for (int i = 0; i <= n; i++)
    {
        for (int j = 0; j <= m; j++)
        {
            if (i == 0 && j == 0)
            {
                continue;
            }

            if (a[i][j] == 0)
            {
                continue;
            }
            if (i == 0)
            {
                a[i][j] = a[i][j - 1];
            }
            else if (j == 0)
            {
                a[i][j] = a[i - 1][j];
            }
            else
            {
                a[i][j] = a[i - 1][j] + a[i][j - 1];
            }
        }
    }

    printf("%d", a[n][m]);
    return 0;
}