在高考中,集合一般会占一个选择题或者一个填空,属于送分题型。但是可能避免不了粗心大意,导致错分。因此,完全熟悉概念、性质、运算、公式等内容是非常重要的 。本篇文章介绍了集合的概念及其性质,以及集合间的基本关系、子集个数、集合的基本运算等内容。
一、原文#
在全国高考中,本节主要考查集合的概念、关系、运算等,下面梳理一些常考知识点.
1、集合中元素的性质#
确定性,互异性,无序性.
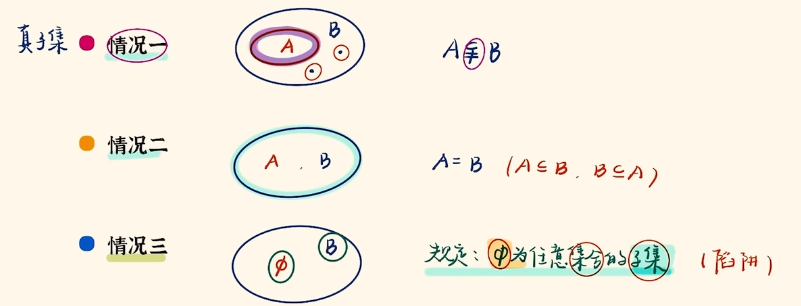
2、集合间的基本关系#
| 关系 | 自然语言 | 符号语言 |
|---|---|---|
| 子集 | 集合 \(A\) 中所有元素都在集合 \(B\) 中 | \(A \subseteq B\) |
| 真子集 | 集合 \(A\) 是集合 \(B\) 的子集,且集合 \(B\) 中至少有一个元素不在集合 \(A\) 中 | \(A \subsetneqq B\) |
| 集合相等 | 集合 \(A\),\(B\) 中的元素相同或集合 \(A\),\(B\) 互为子集 | \(A=B\) |
3、子集个数#
含有 \(n\) 个元素的集合的子集有 \(2^{n}\) 个,非空子集有 \(2^{n}-1\) 个,真子集有 \(2^{n}-1\),非空真子集有 \(2^{n}-2(n\geq 1)\) 个.
4、集合的基本运算#
| 运算 | 自然语言 | 符号语言 |
|---|---|---|
| 并集 | 由所有属于集合 \(A\) 或属于集合 \(B\) 的元素组成的集合 | \(A\cup B=\{x\mid x\in A\) 或 \(x\in B \}\) |
| 交集 | 由属于集合 \(A\) 且属于集合 \(B\) 的所有元素组成的集合 | \(A\cap B = \{x\mid x\in A\) 且 \(x\in B \}\) |
| 补集 | 由全体 \(U\) 中不属于集合 \(A\) 的所有元素组成的集合 | \(\complement_{U}A=\{x\mid x\in U\) 且 \(x\notin A\}\) |
二、原文深度解析#
1、概念#
集合 (set) 简称集,是一个基本的 [数学模型],指 [若干] [不同] [对象] 形成的总体 1
| 名称 | 解释 | 举例 |
|---|---|---|
| 数学模型 | 是使用数学来将一个系统简化后予以描述 | 概率模型 |
| 若干 | 表示不定量 | 零、一、多、无限 |
| 不同 | 互不相同 | \(\{\frac{1}{2},0.5\}\) 不是集合 |
| 对象 | 任何被演绎推理和数学证明正式定义的对象 | 数、集合、函数、表达式、几何形状 |
其他细节:
- 集合里的对象称作元素或成员,它们 可以是任何类型的数学对象 :数字、符号、变量、空间中的点、线、面,甚至是其他集合
- 若 \(x\) 是集合 \(A\) 的元素,记作 \(x\in A\)
- 不包含任何元素的集合称为空集 ;只包含一个元素的集合称为单元素集合
- 集合可以包含 有限或无限个元素
- 如果两个集合所包含的元素完全相同,我们称这两个集合相等.
2、性质#
集合 [元素的性质] 有 [确定性]、[互异性]、[无序性] 2
| 名称 | 解释 | 举例 |
|---|---|---|
| 元素的性质 | 元素之间的性质,不是指集合之间 | 集合没有互异性,两个集合可以相等 |
| 确定性 | 给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现. | 比王俊凯帅的男孩不构成集合 |
| 互异性 | 一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。 | |
| 无序性 | 一个集合中,每个元素的地位都是相同的,元素之间是无序的 |
互异性常考类型:集合相等
已知 \(\{a,\frac{b}{a},1\}=\{a^2,a+b,0\}\),则 \(a^{2022}+b^{2023}=\) ________
两种思考方式:
从待定元素 \(\longrightarrow\) 已知值
当 \(a=a^2\) 时, \(a=-1\)
- 当 \(\frac{b}{a}=a+b\) 时,\(b=\frac{1}{2}\) ,此时 \(\{-1,-\frac{1}{2},1\}=\{1,-\frac{1}{2},0\}\) 不符合题意.
- 当 \(\frac{b}{a}=0\) 时,\(b=0\),此时 \(\{-1,0,1\}=\{1,-1,0\}\) 符合题意
当 \(a=a+b\) 时,\(b=0\),此时 \(\{a,0,1\}=\{a^2,a,0\}\)
所以 \(a^2=1\) 则 \(a=-1\) 此时 \(\{-1,0,1\}=\{1,-1,0\}\) 符合题意
当 \(a=0\) 时,不符合题意
综上,\(a=-1\),\(b=0\)
从已知值 \(\longrightarrow\) 待定元素
从 \(1\) 出发
- 当 \(1=a^2\) 时,\(a=-1\),同上,\(a=-1,b=0\)
- 当 \(1=a+b\) 时,此时只能是 \(b=0\),\(a=1\) 不符合题意
从 \(0\) 出发
只能是 \(b=0\),此时 \(\{a,0,1\}=\{a^2,a,0\}\)
同上 \(a=-1\)
综上,\(a=-1\),\(b=0\)
最优解:
对比总结:
选取最快的思考方法
都有两个待定,如果由此进行分类讨论,情况太多,故选择从已知值 \(\longrightarrow\) 待定元素
选择最快的进入点
如果从 \(1\) 开始,无法立即确定 \(a^2\) 是 \(1\) 还是 \(a+b\) 是 \(1\). 但从 \(0\) 开始,即可立即确定 \(b=0\)
务必验证
求出参数后,务必验证是否满足互异性
3、集合之间的关系#
空集 \(\varnothing\)
空集是什么:
- 年龄大于 \(200\) 岁的活人
- 大于 \(3\) 小于 \(2\) 的实数
- 绝对值等于 \(-1\) 的实数
以上能构成集合,满足集合的性质,但不包含任何元素
空集的简单考法:
已知集合 \(M=\{x\mid 2m<x<m+1\}\),且 \(M\in \varnothing\),则实数 \(m\) 的取值范围是:
因为 \(M\) 是空集,则 \(M\) 中不包含任何元素,即小的反而大,大的反而小
\(2m>m+1\) 还是 \(2m\ge m+1\) ?
大胆猜想,小心求证:先试一下 \(2m=m+1 \longrightarrow m=1\) ,恰好 \(m=1\) 符合题意
问取值范围时要用集合来答,即取值范围是 \(\{m\mid m\ge 1\}\)
集合里有参数,注意空集子集 \( \subseteq \)
如果 [集合 \(A\)] 中任意一个元素都属于 [集合 \(B\)] ,则称集合 \(A\) 是集合 \(B\) 的子集
名称 解释 举例 集合…集合 子集的概念是集合与集合之间 元素不能是一个集合的子集
三、公式证明#
证明:若集合 \(A\) 含有 \(n\) 个元素,则 \(A\) 的子集总个数为 \(f(n)=2^n\)
证法 1 (分类法和递推公式)
第一步:当集合 \(A=\varnothing\) 时,其子集只有空集,\(f(0)=2^0=1\),显然公式成立.
第二步:当集合 \(A\ne \varnothing\) 时,设集合 \(A=\{a_1,a_2,a_3…a_n \}\) 含有 \(n\) 个元素.
则集合 A 的子集可分为两类.
分类 描述 数学语言 第一类 不含有元素 \(a_1\) 的子集 \(\{a_2,a_3,…,a_n\}\) 的所有子集 第二类 含有元素 \(a_1\) 的子集 举个例子:若 \(A =\{1,2,3,4\}\)
则:
\(A\) 的子集有:\(\{1234\}\) 、\(\{123\}\) 、\(\{124\}\) 、\(\{134\}\) 、\(\{234\}\) 、\(\{12\}\) 、\(\{13\}\) 、\(\{14\}\) 、\(\{23\}\)、\(\{24\}\) 、\(\{34\}\)、\(\{1\}\) 、\(\{2\}\) 、\(\{3\}\)、\(\{4\}\)、\(\{\varnothing \}\)
第一类有:\(\{234\}\)、\(\{23\}\)、\(\{24\}\)、\(\{34\}\)、\(\{2\}\)、\(\{3\}\)、\(\{4\}\)、\(\{\varnothing \}\)
第二类有:\(\{1234\}\)、\(\{123\}\)、\(\{124\}\)、\(\{134\}\)、\(\{12\}\)、\(\{13\}\)、\(\{14\}\)、\(\{1 \}\)
第一类共有 \((n-1)\) 个元素,所以共有 \(f(n-1)\) 个子集。
第二类可看作第一类每个子集都添加一个元素 \(a_1\) 而成,所以第二类子集个数 = 第一类子集个数 = \(f(n-1)\)
又由于总子集个数 = 第一类 + 第二类,即
\[f(n)=f(n-1)+f(n-1)=2f(n-1)\]
重复应用上述递推公式可得:
\[f(n)=2f(n-1)= 2^2 f(n-2) = 2^n f(n-n) = 2^n f(0) = 2^n \times 1 = 2^n\]
证毕!
证法 2 (乘法计数原理)
对于集合 \(A\) 中任意子集 \(B\),那么集合 \(A\) 中元素 \(a_i\) 要么 \(a_i \in B\) 要么 \(a_i \notin B\).
根据分步乘法计数原理,从 \(a_1\) 到 \(a_i\) 考虑 \(n\) 步,每一步都有 2 种可能的情况,故 \(A\) 的子集有 \(2^n\) 个.
证法 3 (数学归纳法)
第一步:当 \(n=0,1\) 时,\(f(0)=1\),\(f(1)=2\) 显然公式成立.
第二步:假设当 \(n=k\) 时公式成立,\(f(k)=2^k\)
则当 \(n=k+1\) 时,可设 \(A=\{a_1,a_2,…,a_{k+1}\}\)
此时 \(A\) 的子集可分为两类
分类 描述 子集个数 第一类 不含有 \(a_{k+1}\) 的子集 \(\{a_1,a_2,…a_k\}\) 的子集 = \(f(k)\) 第二类 含有 \(a_{k+1}\) 的子集 \(f(k)\) 则 \(f(k+1)=2f(k)=2^{k+1}\)
所以当 \(n=k+1\) 是公式也成立.
最后根据数学归纳法原理可证得公式对于一切非负整数 \(n\) 都成立.
证法 4 (组合数和二项式定理)
二项式定理:\((a + b)^n = \binom{0}{n} a^n b^0 +\binom{1}{n} a^{n-1} b^{1} + … + \binom{n}{n} a^0 b^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k\)
- 当 \(a=b=1\) 时,等式变为 \((1+1)^n = 2^n = \binom{0}{n} +\binom{1}{n} + … +\binom{n}{n}\)
组合数:从 \(n\) 个不同元素中,不管顺序抽出 \(m\) 个不同元素,其中组合种数称为组合数: \(\binom{m}{n} = \frac{n!}{m! \cdot (n-m)!}\)
首先,设 \(A\) 集合的元素个数为 \(n\),其子集中的组成元素个数为 \(k\).
当 \(k=0\) :\(\varnothing \longrightarrow \binom{0}{n}\)
当 \(k=1\) :\(\{a_1\}\),\(\{a_2\}\) … \(\{a_n\}\) \(\longrightarrow \binom{1}{n}\)
当 \(k=2\) :\(\{a_1,a_2\}\),\(\{a_1,a_3\}\),\(\{a_1,a_4\}\) … \(\longrightarrow \binom{2}{n}\)
当 \(k=n\) :\(\{a_1,a_2,a_3…a_n\}\longrightarrow \binom{n}{n}\)
集合 \(A\) 的子集总个数为:\(\binom{0}{n} +\binom{1}{n} + … +\binom{n}{n} = \sum_{k=0}^{n} \binom{k}{n} = 2^n\)
原视频地址如下:
四、补充#
1、常见数集#
| 数集 | 符号 | 举例 |
|---|---|---|
| 自然数集 | \(N\) | \(0,1,2,\cdots\) |
| 正整数集 | \(N^+\) | \(1,2,3,\cdots\) |
| 整数集 | \(Z\) | \(0,\pm1,\pm2,\pm3,\cdots\) |
| 有理数集 | \(Q\) | |
| 实数集 | \(R\) | 有理数,无理数 |
| 复数集 | \(C\) | \(i\) |
2、集合的表示方法#
列举法
举例 表示 大于 \(1\) 小于 \(5\) 的整数构成的集合 \(\{2,3,4\}\) 绝对值小于 \(3\) 的整数构成的集合 \(\{0,\pm1,\pm2\}\) 所有偶数构成的集合 \(\{0,\pm2,\pm4,\pm6,\cdots\}\) 第一象限的点所构成的集合 无法列举 描述法
举例 表示 大于 \(1\) 小于 \(5\) 的整数构成的集合 \(\{ x\mid 1 < x < 5,x\in Z\}\) 或 \(\{x\in Z\mid 1 < x < 5\}\) 绝对值小于 \(3\) 的整数构成的集合 \(\{x\mid \lvert x\rvert<3,x\in Z\}\) 所有偶数构成的集合 \(\{x\mid x=2k,k\in Z\}\) 第一象限的点所构成的集合 \(\{(x,y) \mid x>0,y>0,x\in R,y\in R\}\)